ref : https://mlwave.com/kaggle-ensembling-guide/
Model ensembling is a very powerful technique to increase accuracy on a variety of ML tasks. In this article I will share my ensembling approaches for Kaggle Competitions.
For the first part we look at creating ensembles from submission files. The second part will look at creating ensembles through stacked generalization/blending.
I answer why ensembling reduces the generalization error. Finally I show different methods of ensembling, together with their results and code to try it out for yourself.
This is how you win ML competitions: you take other peoples’ work and ensemble them together.”
Vitaly Kuznetsov NIPS2014
Creating ensembles from submission files
The most basic and convenient way to ensemble is to ensemble Kaggle submission CSV files. You only need the predictions on the test set for these methods — no need to retrain a model. This makes it a quick way to ensemble already existing model predictions, ideal when teaming up.
Voting ensembles.
We first take a look at a simple majority vote ensemble. Let’s see why model ensembling reduces error rate and why it works better to ensemble low-correlated model predictions.
Error correcting codes
During space missions it is very important that all signals are correctly relayed.
If we have a signal in the form of a binary string like:
1110110011101111011111011011
and somehow this signal is corrupted (a bit is flipped) to:
1010110011101111011111011011
then lives could be lost.
A coding solution was found in error correcting codes. The simplest error correcting code is a repetition-code: Relay the signal multiple times in equally sized chunks and have a majority vote.
Original signal:
1110110011
Encoded:
10,3 101011001111101100111110110011
Decoding:
1010110011
1110110011
1110110011
Majority vote:
1110110011
Signal corruption is a very rare occurrence and often occur in small bursts. So then it figures that it is even rarer to have a corrupted majority vote.
As long as the corruption is not completely unpredictable (has a 50% chance of occurring) then signals can be repaired.
A machine learning example
Suppose we have a test set of 10 samples. The ground truth is all positive (“1”):
1111111111
We furthermore have 3 binary classifiers (A,B,C) with a 70% accuracy. You can view these classifiers for now as pseudo-random number generators which output a “1” 70% of the time and a “0” 30% of the time.
We will now show how these pseudo-classifiers are able to obtain 78% accuracy through a voting ensemble.
A pinch of maths
For a majority vote with 3 members we can expect 4 outcomes:
All three are correct
0.7 * 0.7 * 0.7
= 0.3429
Two are correct
0.7 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.7
= 0.4409
Two are wrong
0.3 * 0.3 * 0.7
+ 0.3 * 0.7 * 0.3
+ 0.7 * 0.3 * 0.3
= 0.189
All three are wrong
0.3 * 0.3 * 0.3
= 0.027
We see that most of the times (~44%) the majority vote corrects an error. This majority vote ensemble will be correct an average of ~78% (0.3429 + 0.4409 = 0.7838).
Number of voters
Like repetition codes increase in their error-correcting capability when more codes are repeated, so do ensembles usually improve when adding more ensemble members.
Using the same pinch of maths as above: a voting ensemble of 5 pseudo-random classifiers with 70% accuracy would be correct ~83% of the time. One or two errors are being corrected during ~66% of the majority votes. (0.36015 + 0.3087)
Correlation
When I first joined the team for KDD-cup 2014, Marios Michailidis (KazAnova) proposed something peculiar. He calculated the Pearson correlation for all our submission files and gathered a few well-performing models which were less correlated.
Creating an averaging ensemble from these diverse submissions gave us the biggest 50-spot jump on the leaderboard. Uncorrelated submissions clearly do better when ensembled than correlated submissions. But why?
To see this, let us take 3 simple models again. The ground truth is still all 1’s:
1111111100 = 80% accuracy
1111111100 = 80% accuracy
1011111100 = 70% accuracy.
These models are highly correlated in their predictions. When we take a majority vote we see no improvement:
1111111100 = 80% accuracy
Now we compare to 3 less-performing, but highly uncorrelated models:
1111111100 = 80% accuracy
0111011101 = 70% accuracy
1000101111 = 60% accuracy
When we ensemble this with a majority vote we get:
1111111101 = 90% accuracy
Which is an improvement: A lower correlation between ensemble model members seems to result in an increase in the error-correcting capability.
Use for Kaggle: Forest Cover Type prediction

Majority votes make most sense when the evaluation metric requires hard predictions, for instance with (multiclass-) classification accuracy.
The forest cover type prediction challenge uses the UCI Forest CoverType dataset. The dataset has 54 attributes and there are 6 classes.
We create a simple starter model with a 500-tree Random Forest. We then create a few more models and pick the best performing one. For this task and our model selection an ExtraTreesClassifier works best.
Weighing
We then use a weighted majority vote. Why weighing? Usually we want to give a better model more weight in a vote. So in our case we count the vote by the best model 3 times. The other 4 models count for one vote each.
The reasoning is as follows: The only way for the inferior models to overrule the best model (expert) is for them to collectively (and confidently) agree on an alternative.
We can expect this ensemble to repair a few erroneous choices by the best model, leading to a small improvement only. That’s our punishment for forgoing a democracy and creating a Plato’s Republic.
“Every city encompasses two cities that are at war with each other.”
Plato in The Republic
Table 1. shows the result of training 5 models, and the resulting score when combining these with a weighted majority vote.
| Model | Public Accuracy Score |
|---|---|
| GradientBoostingMachine | 0.65057 |
| RandomForest Gini | 0.75107 |
| RandomForest Entropy | 0.75222 |
| ExtraTrees Entropy | 0.75524 |
| ExtraTrees Gini (Best) | 0.75571 |
| Voting Ensemble (Democracy) | 0.75337 |
| Voting Ensemble (3*Best vs. Rest) | 0.75667 |
Use for Kaggle: CIFAR-10 Object detection in images

CIFAR-10 is another multi-class classification challenge where accuracy matters.
Our team leader for this challenge, Phil Culliton, first found the best setup to replicate a good model from dr. Graham.
Then he used a voting ensemble of around 30 convnets submissions (all scoring above 90% accuracy). The best single model of the ensemble scored 0.93170.
A voting ensemble of 30 models scored 0.94120. A ~0.01 reduction in error rate, pushing the resulting score beyond the estimated human classification accuracy.
Code
We have a sample voting script you could use at the MLWave Github repo. It operates on a directory of Kaggle submissions and creates a new submission. Update: Armando Segnini has added weighing.
Ensembling. Train 10 neural networks and average their predictions. It’s a fairly trivial technique that results in easy, sizeable performance improvements.
One may be mystified as to why averaging helps so much, but there is a simple reason for the effectiveness of averaging. Suppose that two classifiers have an error rate of 70%. Then, when they agree they are right. But when they disagree, one of them is often right, so now the average prediction will place much more weight on the correct answer.
The effect will be especially strong whenever the network is confident when it’s right and unconfident when it’s wrong.
Ilya Sutskever A brief overview of Deep Learning.
Averaging
Averaging works well for a wide range of problems (both classification and regression) and metrics (AUC, squared error or logaritmic loss).
There is not much more to averaging than taking the mean of individual model predictions. An often heard shorthand for this on Kaggle is “bagging submissions”.
Averaging predictions often reduces overfit. You ideally want a smooth separation between classes, and a single model’s predictions can be a little rough around the edges.

The above image is from the Kaggle competition: Don’t Overfit!, the black line shows a better separation than the green line. The green line has learned from noisy datapoints. No worries! Averaging multiple different green lines should bring us closer to the black line.
Remember our goal is not to memorize the training data (there are far more efficient ways to store data than inside a random forest), but to generalize well to new unseen data.
Kaggle use: Bag of Words Meets Bags of Popcorn

This is a movie sentiment analysis contest. In a previous post we used an online perceptron script to get 95.2 AUC.
The perceptron is a decent linear classifier which is guaranteed to find a separation if the data is linearly separable. This is a welcome property to have, but you have to realize a perceptron stops learning once this separation is reached. It does not necessarily find the best separation for new data.
So what would happen if we initialize 5 perceptrons with random weights and combine their predictions through an average? Why, we get an improvement on the test set!
| Model | Public AUC Score |
|---|---|
| Perceptron | 0.95288 |
| Random Perceptron | 0.95092 |
| Random Perceptron | 0.95128 |
| Random Perceptron | 0.95118 |
| Random Perceptron | 0.95072 |
| Bagged Perceptrons | 0.95427 |
Above results also illustrate that ensembling can (temporarily) save you from having to learn about the finer details and inner workings of a specific Machine Learning algorithm. If it works, great! If it doesn’t, not much harm done.

You also won’t get a penalty for averaging 10 exactly the same linear regressions. Bagging a single poorly cross-validated and overfitted submission may even bring you some gain through adding diversity (thus less correlation).
Code
We have posted a simple averaging script on Github that takes as input a directory of .csv files and outputs an averaged submission. Update: Dat Le has added a geometric averaging script. Geometric mean can outperform a plain average.
Rank averaging
When averaging the outputs from multiple different models some problems can pop up. Not all predictors are perfectly calibrated: they may be over- or underconfident when predicting a low or high probability. Or the predictions clutter around a certain range.
In the extreme case you may have a submission which looks like this:
Id,Prediction
1,0.35000056
2,0.35000002
3,0.35000098
4,0.35000111
Such a prediction may do well on the leaderboard when the evaluation metric is ranking or threshold based like AUC. But when averaged with another model like:
Id,Prediction
1,0.57
2,0.04
3,0.96
4,0.99
it will not change the ensemble much at all.
Our solution is to first turn the predictions into ranks, then averaging these ranks.
Id,Rank,Prediction
1,1,0.35000056
2,0,0.35000002
3,2,0.35000098
4,3,0.35000111
After normalizing the averaged ranks between 0 and 1 you are sure to get an even distribution in your predictions. The resulting rank-averaged ensemble:
Id,Prediction
1,0.33
2,0.0
3,0.66
4,1.0
Historical ranks.
Ranking requires a test set. So what do you do when want predictions for a single new sample? You could rank it together with the old test set, but this will increase the complexity of your solution.
A solution is using historical ranks. Store the old test set predictions together with their rank. Now when you predict a new test sample like “0.35000110” you find the closest old prediction and take its historical rank (in this case rank “3” for “0.35000111”).
Kaggle use case: Acquire Valued Shoppers Challenge

Ranking averages do well on ranking and threshold-based metrics (like AUC) and search-engine quality metrics (like average precision at k).
The goal of the shopper challenge was to rank the chance that a shopper would become a repeat customer.
Our team first took an average of multiple Vowpal Wabbit models together with an R GLMNet model. Then we used a ranking average to improve the exact same ensemble.
| Model | Public | Private |
|---|---|---|
| Vowpal Wabbit A | 0.60764 | 0.59962 |
| Vowpal Wabbit B | 0.60737 | 0.59957 |
| Vowpal Wabbit C | 0.60757 | 0.59954 |
| GLMNet | 0.60433 | 0.59665 |
| Average Bag | 0.60795 | 0.60031 |
| Rank average Bag | 0.61027 | 0.60187 |
I already wrote about the Avito challenge where rank averaging gave us a hefty increase.
Finally, when weighted rank averaging the bagged perceptrons from the previous chapter (1x) with the new bag-of-words tutorial (3x) on fastML.com we improve that model’s performance from 0.96328 AUC to 0.96461 AUC.
Code
A simple work-horse rank averaging script is added to the MLWave Github repo.
Competitions are effective because there are any number of techniques that can be applied to any modeling problem, but we can’t know in advance which will be most effective.
Anthony Goldbloom Data Prediction Competitions — Far More than Just a Bit of Fun
 From ‘How Scotch Blended Whisky is Made’ on Youtube
From ‘How Scotch Blended Whisky is Made’ on Youtube
Stacked Generalization & Blending
Averaging prediction files is nice and easy, but it’s not the only method that the top Kagglers are using. The serious gains start with stacking and blending. Hold on to your top-hats and petticoats: Here be dragons. With 7 heads. Standing on top of 30 other dragons.
Netflix
Netflix organized and popularized the first data science competitions. Competitors in the movie recommendation challenge really pushed the state of the art on ensemble creation, perhaps so much so that Netflix decided not to implement the winning solution in production. That one was simply too complex.
Nevertheless, a number of papers and novel methods resulted from this challenge:
- Feature-Weighted Linear Stacking
- Combining Predictions for Accurate Recommender Systems
- The BigChaos Solution to the Netflix Prize
All are interesting, accessible and relevant reads when you want to improve your Kaggle game.
This is a truly impressive compilation and culmination of years of work, blending hundreds of predictive models to finally cross the finish line. We evaluated some of the new methods offline but the additional accuracy gains that we measured did not seem to justify the engineering effort needed to bring them into a production environment.
Netflix Engineers
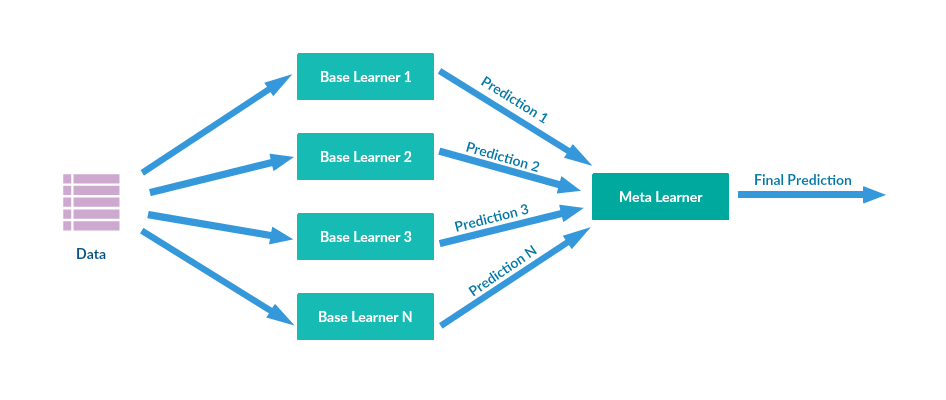
Stacked generalization
Stacked generalization was introduced by Wolpert in a 1992 paper, 2 years before the seminal Breiman paper “Bagging Predictors“. Wolpert is famous for another very popular machine learning theorem: “There is no free lunch in search and optimization“.
The basic idea behind stacked generalization is to use a pool of base classifiers, then using another classifier to combine their predictions, with the aim of reducing the generalization error.
Let’s say you want to do 2-fold stacking:
- Split the train set in 2 parts: train_a and train_b
- Fit a first-stage model on train_a and create predictions for train_b
- Fit the same model on train_b and create predictions for train_a
- Finally fit the model on the entire train set and create predictions for the test set.
- Now train a second-stage stacker model on the probabilities from the first-stage model(s).
A stacker model gets more information on the problem space by using the first-stage predictions as features, than if it was trained in isolation.
It is usually desirable that the level 0 generalizers are of all “types”, and not just simple variations of one another (e.g., we want surface-fitters, Turing-machine builders, statistical extrapolators, etc., etc.). In this way all possible ways of examining the learning set and trying to extrapolate from it are being exploited. This is part of what is meant by saying that the level 0 generalizers should “span the space”.
[…] stacked generalization is a means of non-linearly combining generalizers to make a new generalizer, to try to optimally integrate what each of the original generalizers has to say about the learning set. The more each generalizer has to say (which isn’t duplicated in what the other generalizer’s have to say), the better the resultant stacked generalization.
Wolpert (1992) Stacked Generalization
Blending
Blending is a word introduced by the Netflix winners. It is very close to stacked generalization, but a bit simpler and less risk of an information leak. Some researchers use “stacked ensembling” and “blending” interchangeably.
With blending, instead of creating out-of-fold predictions for the train set, you create a small holdout set of say 10% of the train set. The stacker model then trains on this holdout set only.
Blending has a few benefits:
- It is simpler than stacking.
- It wards against an information leak: The generalizers and stackers use different data.
- You do not need to share a seed for stratified folds with your teammates. Anyone can throw models in the ‘blender’ and the blender decides if it wants to keep that model or not.
The cons are:
- You use less data overall
- The final model may overfit to the holdout set.
- Your CV is more solid with stacking (calculated over more folds) than using a single small holdout set.
As for performance, both techniques are able to give similar results, and it seems to be a matter of preference and skill which you prefer. I myself prefer stacking.
If you can not choose, you can always do both. Create stacked ensembles with stacked generalization and out-of-fold predictions. Then use a holdout set to further combine these models at a third stage.
Stacking with logistic regression
Stacking with logistic regression is one of the more basic and traditional ways of stacking. A script I found by Emanuele Olivetti helped me understand this.
When creating predictions for the test set, you can do that in one go, or take an average of the out-of-fold predictors. Though taking the average is the clean and more accurate way to do this, I still prefer to do it in one go as that slightly lowers both model and coding complexity.
Kaggle use: “Papirusy z Edhellond”

I used the above blend.py script by Emanuele to compete in this inClass competition. Stacking 8 base models (diverse ET’s, RF’s and GBM’s) with Logistic Regression gave me my second best score of 0.99409 accuracy, good for first place.
Kaggle use: KDD-cup 2014
Using this script I was able to improve a model from Yan Xu. Her model before stacking scored ~0.605 AUC. With stacking this improved to ~0.625.
Stacking with non-linear algorithms
Popular non-linear algorithms for stacking are GBM, KNN, NN, RF and ET.
Non-linear stacking with the original features on multiclass problems gives surprising gains. Obviously the first-stage predictions are very informative and get the highest feature importance. Non-linear algorithms find useful interactions between the original features and the meta-model features.
Kaggle use: TUT Headpose Estimation Challenge

The TUT Headpose Estimation challenge can be treated as a multi-class multi-label classification challenge.
For every label a separate ensemble model was trained.
The following table shows the result of training individual models, and their improved scores when stacking the predicted class probabilities with an extremely randomized trees model.
| Model | Public MAE | Private MAE |
|---|---|---|
| Random Forests 500 estimators | 6.156 | 6.546 |
| Extremely Randomized Trees 500 estimators | 6.317 | 6.666 |
| KNN-Classifier with 5 neighbors | 6.828 | 7.460 |
| Logistic Regression | 6.694 | 6.949 |
| Stacking with Extremely Randomized Trees | 4.772 | 4.718 |
We see that stacked generalization with standard models is able to reduce the error by around 30%(!).
Read more about this result in the paper: Computer Vision for Head Pose Estimation: Review of a Competition.
Code
You can find a function to create out-of-fold probability predictions in the MLWave Github repo. You could use numpy horizontal stacking (hstack) to create blended datasets.
Feature weighted linear stacking
Feature-weighted linear stacking stacks engineered meta-features together with model predictions. The hope is that the stacking model learns which base model is the best predictor for samples with a certain feature value. Linear algorithms are used to keep the resulting model fast and simple to inspect.

Vowpal Wabbit can implement a form of feature-weighted linear stacking out of the box. If we have a train set like:
1 |f f_1:0.55 f_2:0.78 f_3:7.9 |s RF:0.95 ET:0.97 GBM:0.92
We can add quadratic feature interactions between the s-featurespace and the f-featurespace by adding -q fs. The features in the f-namespace can be engineered meta-features like in the paper, or they can be the original features.
Quadratic linear stacking of models
This did not have a name so I made one up. It is very similar to feature-weighted linear stacking, but it creates combinations of model predictions. This improved the score on numerous experiments, most noticeably on the Modeling Women’s Healthcare Decision competition on DrivenData.
Using the same VW training set as before:
1 |f f_1:0.55 f_2:0.78 f_3:7.9 |s RF:0.95 ET:0.97 GBM:0.92
We can train with -q ss creating quadratic feature interactions (RF*GBM) between the model predictions.
This can easily be combined with feature-weighted linear stacking: -q fs -q ss, possibly improving on both.
So now you have a case where many base models should be created. You don’t know apriori which of these models are going to be helpful in the final meta model. In the case of two stage models, it is highly likely weak base models are preferred.
So why tune these base models very much at all? Perhaps tuning here is just obtaining model diversity. But at the end of the day you don’t know which base models will be helpful. And the final stage will likely be linear (which requires no tuning, or perhaps a single parameter to give some sparsity).
Mike Kim Tuning doesn’t matter. Why are you doing it?
Stacking classifiers with regressors and vice versa
Stacking allows you to use classifiers for regression problems and vice versa. For instance, one may try a base model with quantile regression on a binary classification problem. A good stacker should be able to take information from the predictions, even though usually regression is not the best classifier.
Using classifiers for regression problems is a bit trickier. You use binning first: You turn the y-label into evenly spaced classes. A regression problem that requires you to predict wages can be turned into a multiclass classification problem like so:
- Everything under 20k is class 1.
- Everything between 20k and 40k is class 2.
- Everything over 40k is class 3.
The predicted probabilities for these classes can help a stacking regressor make better predictions.
“I learned that you never, ever, EVER go anywhere without your out-of-fold predictions. If I go to Hawaii or to the bathroom I am bringing them with. Never know when I need to train a 2nd or 3rd level meta-classifier”
T. Sharf
Stacking unsupervised learned features
There is no reason we are restricted to using supervised learning techniques with stacking. You can also stack with unsupervised learning techniques.
K-Means clustering is a popular technique that makes sense here. Sofia-ML implements a fast online k-means algorithm suitable for this.
Another more recent interesting addition is to use t-SNE: Reduce the dataset to 2 or 3 dimensions and stack this with a non-linear stacker. Using a holdout set for stacking/blending feels like the safest choice here. See here for a solution by Mike Kim, using t-SNE vectors and boosting them with XGBoost: ‘0.41599 via t-SNE meta-bagging‘.
Piotr shows a nice visualization with t-SNE on the Otto Product Classification Challenge data set.Online Stacking
I spend quit a lot of time working out an idea I had for online stacking: first create small fully random trees from the hashed binary representation. Substract profit or add profit when the tree makes a correct prediction. Now take the most profitable and least profitable trees and add them to the feature representation.
It worked, but only on artificial data. For instance, a linear perceptron with online random tree stacking was able to learn a non-linear XOR-problem. It did not work on any real-life data I tried it on, and believe me, I tried. So from now on I’ll be suspicious of papers which only feature artificial data sets to showcase their new algorithm.
A similar idea did work for the author of the paper: random bit regression. Here many random linear functions are created from the features, and the best are found through heavy regularization. This I was able to replicate with success on some datasets. This will the topic of a future post.
A more concrete example of (semi-) online stacking is with ad click prediction. Models trained on recent data perform better there. So when a dataset has a temporal effect, you could use Vowpal Wabbit to train on the entire dataset, and use a more complex and powerful tool like XGBoost to train on the last day of data. Then you stack the XGBoost predictions together with the samples and let Vowpal Wabbit do what it does best: optimizing loss functions.
The natural world is complex, so it figures that ensembling different models can capture more of this complexity.
Ben Hamner ‘Machine learning best practices we’ve learned from hundreds of competitions’ (video)
Everything is a hyper-parameter
When doing stacking/blending/meta-modeling it is healthy to think of every action as a hyper-parameter for the stacker model.
So for instance:
- Not scaling the data
- Standard-Scaling the data
- Minmax scaling the data
are simply extra parameters to be tuned to improve the ensemble performance. Likewise, the number of base models to use can be seen as a parameter to optimize. Feature selection (top 70%) or imputation (impute missing features with a 0) are other examples of meta-parameters.
Like a random gridsearch is a good candidate for tuning algorithm parameters, so does it work for tuning these meta-parameters.
Sometimes it is useful to allow XGBoost to see what a KNN-classifier sees. –
Marios Michailidis
Model Selection
You can further optimize scores by combining multiple ensembled models.
- There is the ad-hoc approach: Use averaging, voting or rank averaging on manually-selected well-performing ensembles.
- Greedy forward model selection (Caruana et al.). Start with a base ensemble of 3 or so good models. Add a model when it increases the train set score the most. By allowing put-back of models, a single model may be picked multiple times (weighing).
- Genetic model selection uses genetic algorithms and CV-scores as the fitness function. See for instance inversion‘s solution ‘Strategy for top 25 position‘.
- I use a fully random method inspired by Caruana’s method: Create a 100 or so ensembles from randomly selected ensembles (without placeback). Then pick the highest scoring model.
Automation

When stacking for the Otto product classification competition I quickly got a good top 10 spot. Adding more and more base models and bagging multiple stacked ensembles I was able to keep improving my score.
Once I had reached 7 base models stacked by 6 stackers, a sense of panic and gloom started to set in. Would I be able to replicate all of this? These complex and slow unwieldy models were out of my comfort zone of fast and simple Machine Learning.
I spend the rest of the competition building a way to automate stacking. For base models pure random algorithms with pure random parameters are trained. Wrappers were written to make classifiers like VW, Sofia-ML, RGF, MLP and XGBoost play nicely with the Scikit-learn API.

The first whiteboard sketch for a parallelized automated stacker with 3 buckets
For stackers I let the script use SVM, random forests, extremely randomized trees, GBM and XGBoost with random parameters and a random subset of base models.
Finally the created stackers are averaged when their fold-predictions on the train set produced a lower loss.
This automated stacker was able to rank 57th spot a week before the competition ended. It contributed to my final ensemble. The only difference was I never spend time tuning or selecting: I started the script, went to bed, and awoke to a good solution.
The automated stacker is able to get a top 10% score without any tuning or manual model selection on a competitive task with over 3000 competitors.Automatic stacking is one of my new big interests. Expect a few follow-up articles on this. The best result of automatic stacking was found on the TUT Headpose Estimation challenge. This black-box solution beats the current state-of-the-art set by domain experts who created special-purpose algorithms for this particular problem.
Noteworthy: This was a multi-label classification problem. Predictions for both “yaw” and “pitch” were required. Since the “yaw” and “pitch”-labels of a head pose are interrelated, stacking a model with predictions for “yaw” increased the accuracy for “pitch” predictions and vice versa. An interesting result.
Models visualized as a network can be trained used back-propagation: then stacker models learn which base models reduce the error the most.

Next to CV-scores one could take the standard deviation of the CV-scores into account (a smaller deviation is a safer choice). One could look at optimizing complexity/memory usage and running times. Finally one can look at adding correlation into the mix — make the script prefer uncorrelated model predictions when creating ensembles.
The entire automated stacking pipeline can be parallelized and distributed. This also brings speed improvements and faster good results on a single laptop.
Contextual bandit optimization seems like a good alternative to fully random gridsearch: We want our algorithm to start exploiting good parameters and models and remember that the random SVM it picked last time ran out of memory. These additions to stacking will be explored in greater detail soon.
In the meantime you can get a sneak preview on the MLWave Github repo: “Hodor-autoML“.
The #1 and #2 winners of the Otto product classification challenge used ensembles of over a 1000 different models. Read more about the first place and the second place.
Why create these Frankenstein ensembles?
You may wonder why this exercise in futility: stacking and combining 1000s of models and computational hours is insanity right? Well… yes. But these monster ensembles still have their uses:
- You can win Kaggle competitions.
- You can beat most state-of-the-art academic benchmarks with a single approach.
- You can then compare your new-and-improved benchmark with the performance of a simpler, more production-friendly model
- One day, today’s computers and clouds will seem weak. You’ll be ready.
- It is possible to transfer knowledge from the ensemble back to a simpler shallow model (Hinton’s Dark Knowledge, Caruana’s Model Compression)
- Not all base models necessarily need to finish in time. In that regard, ensembling introduces a form of graceful degradation: loss of one model is not fatal for creating good predictions.
- Automated large ensembles ward against overfit and add a form of regularization, without requiring much tuning or selection. In principle stacking could be used by lay-people.
- It is currently one of the best methods to improve machine learning algorithms, perhaps telling use something about efficient human ensemble learning.
- A 1% increase in accuracy may push an investment fund from making a loss, into making a little less loss. More seriously: Improving healthcare screening methods helps save lives.
Update: Thanks a lot to Dat Le for documenting and refactoring the code accompanying this article. Thanks to Armando Segnini for adding weighted averaging. Thanks a lot everyone for the encouraging comments. My apologies if I have forgotten to link to your previous inspirational work. Further reading at “More is always better – The power of Simple Ensembles” by Carter Sibley, “Tradeshift Benchmark Tutorial with two-stage SKLearn models” by Dmitry Dryomov, “Stacking, Blending and Stacked Generalization” by Eric Chio, Ensemble Learning: The wisdom of the crowds (of machines) by Lior Rokach, and “Deep Support Vector Machines” by Marco Wiering.
Terminology: When I say ensembling I mean ‘model averaging’: combining multiple models. Algorithms like Random Forests use ensembling techniques like bagging internally. For this article we are not interested in that.The intro image came from WikiMedia Commons and is in the public domain, courtesy of Jesse Merz.Cite
If you use significant portions or methods from this article in a scientific paper, report, or book, please consider attributing with:
- Hendrik Jacob van Veen, Le Nguyen The Dat, Armando Segnini. 2015. Kaggle Ensembling Guide. [accessed 2018 Feb 6]. https://mlwave.com/kaggle-ensembling-guide/
or, if you prefer a more authoritative reference:
- Michailidis, Marios. (2017). Investigating machine learning methods in recommender systems (Thesis). University College London.
For other, less formal, material, such as blogs or educational slides, a simple link will suffice to satisfy Creative Commons 3.0 attribution.
The resource URL will remain static and the page hosted on this site for the foreseeable future.